kd树可能是我们最熟悉的空间索引。kd树的全称是k-dimensional tree,顾名思义,是一种将多维数据组织起来的数据结构。不仅服务于计算几何领域,而且在统计分析、机器学习领域都是非常活跃的。本文将主要围绕kd树的结构、构建、半径搜索(范围搜索)、最近邻搜索(KNN)等主要的算法进行展开,同时也会涉及到近似最近邻与最近邻算法的区别,spliting 策略等有趣的细节。并且,我还会介绍部分FLANN库(被PCL使用)对上述算法的实现方式。在文章末尾,提供了c++实现代码。
1.kd树的结构
kd树是一种二叉树。并且与二分查找树(BST)比较类似。BST可以将一组实数递归的进行划分,类似的,在每一层上kd树沿着按照某个维度将数据分为两组,两组数据依次进行分割形成子树。分割的对象称之为超平面(hyperplane),超平面垂直与对应维度的轴。理想的超平面是对应维度的中位数(median),这样可以保证树的平衡(balance),从而降低树的深度。
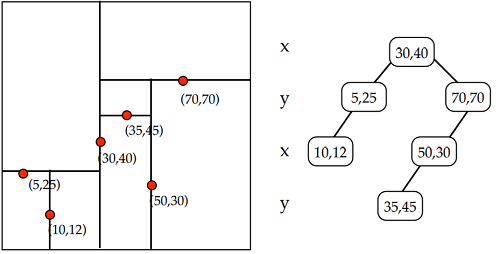
下图所示,是k=2时的一颗kd树。需要提醒的是进行划分(split)的维度的顺序可以是任意的,不一定按照x,y,z,x,y,z…的顺序进行。每一个节点都会记录划分的维度。FLANN中有划分维度选择的算法。
2.kd树的构建(construction)
kd树的构建是采用的是非常典型的递归方法。可以用下面的伪代码表示。其中,递归终止条件是输入的点的个数小于叶子节点最大点个数;而递归的部分是将输入点在中位数处分为两个部分,分别构建左右子树。
Node BuildTree(vector<int> inputs,int start,int end)
{
int size = end - start;
Dimension dim = SelectDimension(inputs,start,end);
int median = Partition(inputs,start,end,dim);
Node* pNode = new Node(inputs,start,end,dim,median);
if(size > _leaf_max_size)
{
pNode->left = BuildTree(inputs,start,median);
pNode->right = BuildTree(inputs,median,end);
}
}
具体实现代码可以到本文最后一节获取。
现在有两个具体的问题需要考虑:
2.1 怎样选择哪一维度进行划分
在《computational geometry》(Mark de Berg等著)一书中,将kd树的维度划分与树的深度关联,比如 维度 = 深度%总维度,这样,kd树的维度划分就保持x,y,z,…,x,y,z…的顺序。很多网上的其他实现也是如此。实际上,并不一定要保持这样的顺序。而且,不同的划分顺序,往往能给kd树的效率带来影响。
因为点数与维数是固定的,kd树的深度(depth)也是固定的,如果采用均匀划分的方式,在分散程度比较小的维度上过度划分,势必会造成分散维度较大的维度划分不充分,更容易导致“长条形”区域出现。在各维度查询概率相同的情况下,长条形肯定更容易被命中,导致被查询次数过多而效率不佳。
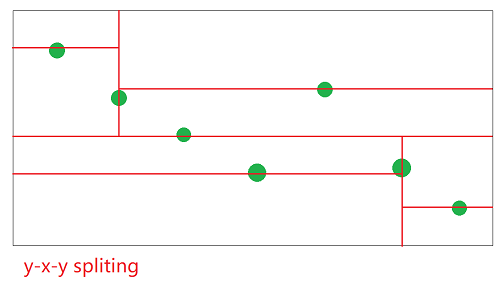
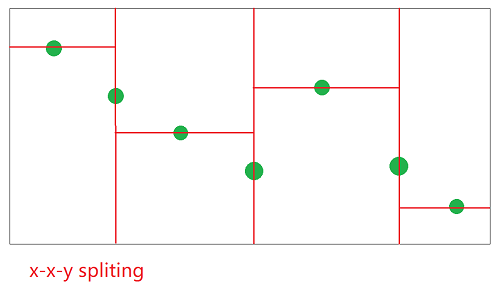
以上两图为例,同样的输入数据(二维),采用y-x-y的划分方式与x-x-y的方式得到的效果,可以看到,后一种划分比较充分,从而查询涉及无关分支的情况比较小,查询效率可能会比较高(具体高不高要看查询范围是不是趋向于正方形)。
2.2 如何减小partition 中swap引发的性能问题 以及 FLANN的解决方案
在kd树的构建中,涉及到了频繁的依据超平面进行分割的问题。因为kd树是面向高维数据的,高维数据的点的尺寸通常比较大,如果直接针对数据本身进行swap,那么会多次调用点数据本身的拷贝赋值函数,开销比较大。有没有比较合适的的方法?
其一就是采用指针作为数组元素,而不是对象本身,这样 指针的swap就要廉价很多了。但是这样的话,相当于对输入数据就有要求了,恐怕适用性不强。
还有一种方法就是FLANN使用的方式,比较提倡使用。具体方法是,由使用kd树者持有数据,传给kd树的是与输入数据points等长的index数组indices,indices[i] 标识数据的索引,因此调整后的 p_i = points[indices[i]] 当数组partition的时候,调整的只是 indices的数值,开销就要小很多了,而且调用者持有的数据的顺序并没有发生改变。
这样,可以给出一种kdtree::Node 的设计:
namespace kdtree
{
class Node
{
public:
Node* left; //left child
Node* right; //right child
int begin; //start index [close
int end; //end index (open
int dimension; //cut dimension
double pivot; //cut value
};
}
2.3 超平面确定算法
前文我们提到,最理想的超平面是中位数。确定中位数的算法有若干种。几年前我最初实现kd树的时候,曾经采用 std::sort 实现,其实是一种非常浪费的方式,因为中位数并不要求数据完全排序,而是要求在中位数左侧的数据不大于中位数,中位数右侧的数据不小于中位数而已。显然,复杂度为O(nlogn)的排序算法用力过度了。实现中位数分割的最佳算法是std::nth_element, 其算法复杂度为O(n) ,系数为2左右。是非常理想的。
FLANN的设计是:根据数据的范围确定首尾(最小最大值)平均值,根据首尾均值将数据分割成三部分,“中位数”的取值由以下几种情况判断产生:
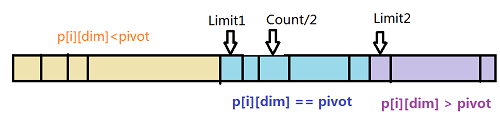
flann 的 median 算法
- 当 limit1 > count/2时,median = limit1;
- 否则当 limit2 < count2时 median = limit2;
- 否则 median = count/2;
这种方式 的复杂度也为\(O(n))\,但是系数较低,比nth_element的速度快。不过,这种方法也存在问题。当输入数据分布不均匀时,采用首尾平均值进行划分的方式很容易导致树不均衡从而使得树的深度增加,查询效率降低。
3. 范围查询(Range Search)、半径查询(Redius Search)
范围查询与半径查询差异不大,可以放在一起讲。
因为KD树本质上是一种树,因此我们的空间查询(包括最近邻查询,范围查询等)都是树遍历算法的一种。如果树不是一种BST,那么查询一次可能要遍历整个树,并不能起到加速作用。KD树与其他树结构的空间索引的作用就是在根节点可以判断子树的情况,在根节点可以判断下一步的搜索方向,完全不必要搜索的节点不会遍历,这样,索引起到了加速查询的作用。
具体到KD树,我们需要解决的现实问题就是节点空间范围的确定。在2.2节Node点的设计上,并没有记录Node的空间范围。这是因为每个Node的范围可以在树的遍历过程中同步完成,并不需要特别记录。
region(lc(v)) = region(v)\cap l(v)^{left}
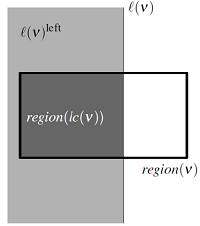
上图是 《computational geometry》中左子树范围确定的方法。右子树与之类似。
因此,一个RangeSearch就是一个树的后序遍历算法的改版。伪代码如下所示(实现代码在文末)
RangeSearch(BBox searchBox,Node* pNode,BBox current_extent)
{
if(pNode->isLeaf())
{
//report all points that within searchBox
}else
{
BBox leftregion;//leftregion 的范围是 current_extent trim 掉 pNode->pivot
if(searchBox.contains(leftregion))
{
//report all points in pNode->left;
}
else if(searchBox.intersects(leftregion))
{
RangeSearch(searchBox,pNode->left,leftregion);//recursive call
}
BBox rightregion; //rightregion 的范围是 current_extent trim pNode->pivot
if(searchBox.contains(rightregion))
{
//report all points in pNode->right;
}else if(searchBox.intersects(rightregion))
{
RangeSearch(searchBox,pNode->right,rightregion);//recursive call
}
}
}
半径查询(radius search)可以完全类比上面的算法进行实现,只不过查询区域需要从 range search的 bounding box 换成 圆或球体(根据维度),同时需要实现contains,intersects等方法。
4.最近邻查询(Nearest Neighbour)
按照问题的复杂程度,可以分解为两个方面 1-NN与 k-NN,分别表示距离搜索点最近的一个点以及最远的k个点。两者的算法类似,k-NN可以在1-NN基础上略作修改得到。
4.1 1-NN
最近邻查询与范围查询不同。可以说rangesearch(radius search)的情况是“固定”的,通过搜索范围与当前节点的范围进行比对,就可以得到固定的搜索路径。而最近邻的情况不同。最近邻在搜索时维护了与搜索点最近的叶子的距离,通过判断搜索点到其他节点的距离的下界“剪掉”没有必要访问的节点。
维护一个搜索点到目前找到最近叶子节点的最小值shortestDistance,初始值为DOUBLE_MAX;
计算搜算点到 当前节点的外界矩形的最小距离min\_shorest\_dis,如果这个距离超过了shortestDistance,那么这个节点没有必要搜索,因为min\_shorest\_dis代表的就是当前节点中所有点到目标节点的最小值的下界。
- 如果当前节点为叶子节点,则更新最小值和最小距离。
- 如果当前节点非叶子节点,则从两个子节点中优选一个(英文称为priorty search)一个节点优先进行搜索,然后再搜索另外一个节点。这一步非常体现出NN “动态”的特性,如果前面更新了最短距离,那么后面就可以“剪掉”一些不必要的节点了。为什么还要搜索后一个节点呢?因为“优选”的节点不一定真正包含最近点。如下图所示:优选节点在left,但是最近点在right。
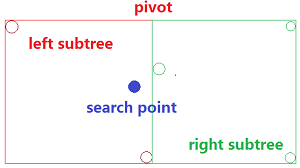
- 按照搜索顺序,后一次如果找到更近的,则使用后一次搜索的结果,没有则取前一次的。
最近邻搜索的伪代码如下:
int NearestNeighbour(Point searchPoint,Node* pNode,const BBox& current_extent, double& shortestDistance)
{
/**
搜索点到subtree外接矩形的距离表示了点到sutree 中所有点最小距离的下界,
就是说最近距离一定不小于这个数,如果这个数比当前的最小距离 shortestDistance 还大
整个子树就可以不用访问了,起到了加速作用
*/
double min_shortest_dis = shortestDistance(searchPoint,current_extent);
if(min_shortest_dis >= shortestDistance)
return -1;
if(pNode->isLeaf())
{
//find points with shortest distance to searchPoint
//TO-DO Update shortestDistance
return nearestneighbour_index;
}else
{
BBox leftRegion; //leftRegion 由 current_extent trim得到
double dis_to_left = ShorestDistance(searchPoint,leftRegion);
BBox rightRegion;//rightRegion 由 current_extent trim 得到
double dis_to_right = ShorestDistance(searchPoint,rightRegion);
/**
确定left,right 优先查询哪一块,当然是拥有更近距离的具有 priority
但是,这也仅为优先权而已,不能靠其拥有最可能最近邻而排出另一子树
*/
if(dis_to_left<dis_to_right)
{
int left = NearestNeighbour(searchPoint,pNode->left,leftRegion,shortestDistance);
int right = NearestNeighbour(searchPoint,pNode->rihgt,rightRegion,shortestDistance);
return right == -1 ? left : right;
}else
{
int right = NearestNeighbour(searchPoint,pNode->rihgt,rightRegion,shortestDistance);
int left = NearestNeighbour(searchPoint,pNode->left,leftRegion,shortestDistance);
return left == -1? right:left;
}
}
return -1;//dummy
}
这里面会有一个子问题需要解决,点到外接矩形(或者更高维度的范围)的最近距离如何判断。我们规定,如果点在矩形内部(或矩形上)则认为点到矩形的距离为0.这种情况下,stackoverflow 上有对应的解决方案:stackoverflow上对点到 矩形(外侧)最近距离的实现
4.2 k-NN
k-NN与1-NN的整体思路并没有大的区别,增加的部分是,k-NN需要维护一个当前最近点列表nearest_neighbors,并且使nearest_neighbors中的距离最远点(FLANN中称为worest distance)更新 shortestDistance。当有更近点时,使其加入nearest_neighbors,并且使用nearest_neighbors 中的最远点更新shortestDistance。两点需要注意:
- 当nearest_neighbors的size不足k时,不能使用其中最远点更新shortestDistance。
- 因为频繁取距离最大值,建议采用std::priority_queue 实现,其 push() ,pop() 方法复杂度为O(log(n)),top() 方法复杂的为O(1)。
5.近似最近邻查询(Approximate Nearest Neighbor)
FLANN的全称是 “Fast Library for Approximate Nearest Neighbors” ,其中的“Approximate”指的是什么呢?其实我们知道,NN过滤Node的条件是当前搜索半径(最短距离) r 低于 点到 Node外接矩形的距离,ANN通过将 r 除以 大于1的系数\alpha,使得Node 更容易被过滤,从而加快了查询速度,但是得到的结果也是近似的最近点。根据参考文献,ANN能使 NN的查询速度提高10-100倍。
参考文献三对ANN的解释最为直观:
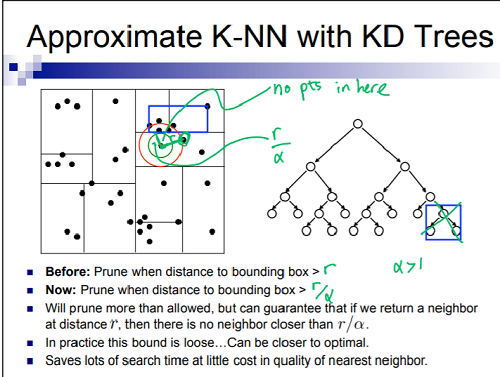
在FLANN中,可以看到 kdtree 拥有接口 setEpsilon (float eps) 设置epsilon 。\epsilon对应上式中的 \alpha = \epsilon+1。不经设置的话,epsilon默认值为0。
6.参考文献:
https://www.cs.cmu.edu/~ckingsf/bioinfo-lectures/kdrangenn.pdf
https://www.cs.cmu.edu/~ckingsf/bioinfo-lectures/kdtrees.pdf
https://courses.cs.washington.edu/courses/cse599c1/13wi/slides/lsh-hashkernels-annotated.pdf
7.实现代码:
