空间关系描述是GIS系统的基本功能之一。我在学校学习到的空间关系分为三种：方位关系、距离关系、拓扑关系。今天我要分享的拓扑关系的标准化描述：9交叉模型。科班出身的GISer可能都知道9交模型是Egenhofer在《point set topological spatial relations》中提出的，不过，我今天不打算综述空间关系有关的理论发展，而是结合geos,分享9交模型的原理以及常见的拓扑关系描述符。

1）9交叉模型的定义

已知两个几何对象A，B(geos中称Geometry)，如何描述A与B的拓扑关系?就交叉模型给出的解决方案是通过描述A与B的内部(Interior , I)，边界(Boundary , B)，外部(Exterior , E)之间的关系来表达A与B的拓扑关系，内部(I)、边界(B)、外部(E)三者的关系构成了一个\(3\times3\)的交集矩阵：$$DE9IM(a,b)=\begin{bmatrix}
dim(I_A\cap I_B)&dim(I_A\cap B_B)&dim(I_A\cap E_B)\\
dim(B_A\cap I_B)&dim(B_A\cap B_B)&dim(B_A\cap E_B)\\
dim(E_A\cap I_B)&dim(E_A\cap B_B)&dim(E_A\cap E_B)\end{bmatrix}$$

2)维度 Dimension

dim是dimension的缩写，指的是维度。在计算几何中，维度是几何要素的重要信息之一，通过维度，可以进行一些判断。比如，高维度的要素(比如线)，是不可能within在低维度的要素中的(比如点)。再比如，两个要素的交集的维度不会超过两者维度中最小者。在geos中(以及其他类似系统)：

1. 多边形的维度是2，含组合多边形，带洞多边形等。
2. 折线的维度为1，含多线。
3. 点的维度为0，含多点。
4. 空集(无交集)维度为F。

讲到这里，我们有必要了解不同类型的几何对象的内部，边界，外部各指的是什么。

3）内部，边界，外部的定义

对于多边形，内部是多边形的外环和内环围起来的面部分，边界由内环和外环构成，外部是除内部和边界以外的空间其他所有部分。

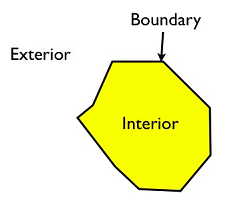
对于线要素，边界是线首尾节点(中间节点不算)，内部是线上除了首尾节点之外的部分。外部是空间除了内部与边界的部分。

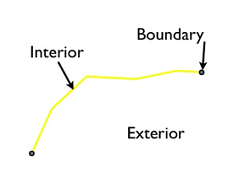
点要素的内部是点本身，其边界是空集，外部是除了点本身外的空间其他部分。当然，对于点与其他要素的拓扑关系，我们通常习惯用“点在对象上”、“点不在对象上”进行描述，而且，在空间关系的计算上，也会按照这样的思路设计算法。我的意思是，对于点的拓扑关系处理一般先判断“点是否在对象上”然后填充9交叉模型矩阵的，而不是像多边形之间的关系判断。

4）9交叉模型的布尔形式

9交叉模型交集矩阵的定义域为{F,0,1,2}，那么一共可能有\(4^9\)种可能的拓扑关系。简单的考虑到外部与外部的交集的维度一定是2 ，那么可能的拓扑关系仍有\(8^9\)种，考虑很多种关系是矛盾的，剩下的组合仍然很多。这与我们希望直观，简单的表达拓扑关系的目标相差甚远。实际上，常见的拓扑关系描述符大概10种左右。为了方便描述这些关系，可以对矩阵的定义域做补充：

1. 0,1,2表示非空，用T进行表示；
2. 空集仍然用F表示；
3. 引入*表示是什么都可以，geos中为“DONTCARE”

我们常用的拓扑关系描述符，就是采用上述6种类型描述出来的。

5）常用拓扑关系描述

Intersects

相交是指两对象的内部或边界存在交集，对应下面四种Intersection Matrix$$\begin{bmatrix}
T&*&*\\
*&*&*\\
*&*&*
\end{bmatrix}$$$$\begin{bmatrix}
*&T&*\\
*&*&*\\
*&*&*
\end{bmatrix}$$$$\begin{bmatrix}
*&*&*\\
T&*&*\\
*&*&*
\end{bmatrix}$$$$\begin{bmatrix}
*&*&*\\
*&T&*\\
*&*&*
\end{bmatrix}$$就是说 对应Interior,Boundary的\(2\times 2\)的部分任意一个单元是T就可以了，其他的都“DONTCARE”。注意，这些矩阵都是对称的。

Disjoint

相离就是不相交，因此对应于相交的“Interior,Bountry  任意存在交集”，相离的定义是Interior,Boundary均不存在交集。$$\begin{bmatrix}
F&F&*\\
F&F&*\\
*&*&*
\end{bmatrix}$$，这个矩阵也是对称的。

Contains

A.Contains(B)表示B完全在A内部。即A,B的interior相交并且 B的Interior与Boundary均不与A的exterior相交。$$\begin{bmatrix}
T&*&*\\
*&*&*\\
F&F&*
\end{bmatrix}$$

Within

Within 与Contains互为转置。A.Contains(B) = B.Within(A)。为什么叫互为转置呢，这是因为within的相交矩阵是Contains矩阵的转置就好了。$$\begin{bmatrix}
T&*&F\\
*&*&F\\
*&*&*
\end{bmatrix}$$

Equal

Equal表示的是A和B的形状完全相同(但是，不是说他们所有的坐标都是完全一样的！A或者B都可能有冗余的坐标，比如多点共线)。Equal的交集矩阵是内部相交，但任意一方的内部与边界均不与对方的外界相交$$\begin{bmatrix}
T&*&F\\
*&*&F\\
F&F&*
\end{bmatrix}$$

Overlap

叠置判断对A与B的维度有要求，要求A与B的维度相同，并且要求A与B的内部的交集的维度与AB的维度相同。因为多边形(面)之间的交集，点之间的交集均与他们的维度相同，线之间的交集可能会是点，线两种情况，所以特别将线与面、点之间的矩阵进行了区分,要求线的内部交集为线。

面、点的交集矩阵：$$\begin{bmatrix}
T&*&T\\
*&*&*\\
T&*&*
\end{bmatrix}$$

线的交集矩阵:$$\begin{bmatrix}
1&*&T\\
*&*&*\\
T&*&*
\end{bmatrix}$$

Touch

Touch表示的是两个几何要素之间的临接关系。touch关系的要点是：

两个元素的内部(interior)不能有交集,但是内部与边界，边界与边界可以有交集。

参与的两种元素不能同时为点类型。(点没有边界，内部与内部不相交变成相离了)

$$\begin{bmatrix}
F&T&*\\
*&*&*\\
*&*&*
\end{bmatrix}$$$$\begin{bmatrix}
F&*&*\\
T&*&*\\
*&*&*
\end{bmatrix}$$$$\begin{bmatrix}
F&*&*\\
*&T&*\\
*&*&*
\end{bmatrix}$$三个矩阵中，前两个互为转置关系，最后一个是对称矩阵。所以说这个关系也是对称的。

Cross 

穿越的定义是A与B的内部有交集，但交集的维度要比A与B最大的维度要小。按照这个标准，点点与面面不可能存在cross关系，因为他们内部的交集的维度与他们的维度是相同的。同样，对于线线的交集要区别对待，指定其内部的交集为0(而不是1)。

非线线交集矩阵：$$\begin{bmatrix}
T&*&T\\
*&*&*\\
*&*&*
\end{bmatrix}$$线线交集矩阵：$$\begin{bmatrix}
0&*&*\\
*&*&*\\
*&*&*
\end{bmatrix}$$

6)对拓扑关系的分析：从矩阵的角度

从上述9交叉模型矩阵的表达上，我们已经能够分析出很多有趣的信息了。

1.如果交集矩阵是对称的，那么对应的拓扑关系满足交换律的。A.Relation(B)=B.Relation(A)

可以交换的拓扑关系有(对应矩阵对称)：

Intersects,Disjoint,Equal,Overlap,Touch,Cross(线线)

不可以交换的拓扑关系有：

Contains,Within,Cross(非线线)

2.如果两个关系矩阵互为转置，那么这两个关系可以调换位置A.Relation1(B)=B.Relation2(A)。满足条件的关系有

Contains,Within

3.如果两个矩阵互补，那么两种关系也是互斥关系。满足条件的有

Intersects,Disjoint

4.拓扑关系之间的关系

上述8种关系并全不是互斥的，元素A,B可以同时满足多种拓扑关系。这些拓扑关系的“关系”更适合使用文氏图来描述：

---

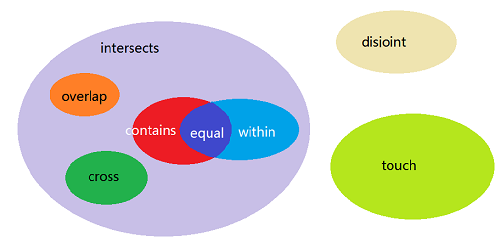
参考文档：

Dimensionally Extended 9-Intersection model(内部、边界、外部定义的图片来源)

Esri doc:Understanding spatial relations

ArcGIS Desktop Help: Spatial Relations