插值是指：已知形状点(Fit Point),求一条样条曲线穿过所有的形状点。插值是B样条乃至CAGD应用中最常见的应用之一。本节，我将分享一种样条曲线插值算法。

我们的条件是，已知点集\(\{F_0,F_1,…,F_x\}\)共x+1个点，求样条曲线\(\sum N_{i,p}P_i\)通过上述所有点\(F_i\)。回顾B样条的定义，可以将上述条件转换为下式：$$\begin{bmatrix}N_{0}(u_0)&…&N_{i}(u_0)&…&N_{p}(u_0)\\N_{0}(u_1)&…&N_{i}(u_1)&…&N_{p}(u_1)\\\cdots\\N_{0}(u_x)&…&N_{i}(u_x)&…&N_{p}(u_)\end{bmatrix}\begin{bmatrix}P_0\\…\\P_i\\…\\P_n\end{bmatrix}=\begin{bmatrix}F_0\\F_1\\\cdots\\F_x\end{bmatrix}$$总结起来就是 \(C(u_i)=F_i\)。那么，首先我们要做就是确定参数，给\(F_i\)确定\(u_i\)的过程，称之为参数化(Parameterization)。

1）参数化

常见的参数化方法有三种：弦长累加法(chord length),向心参数法(也称平方根法)，统一节点法。其中前两种最为常用。

1. 弦长累加法：指的是，当前型值点\(F_i\)的参数，等于之前所有型值点长度的累加\(\sum_{j=1}^{i}|F_{j-1}F_j|\)。这种方法是“Arc-Length”参数法的一种近似，选用弦长代替弧长，因此具有比较好的效果。
2. 向心参数法：这个方法由波音公司的技术人员提出。指的是当前型值点的参数是由之前所有型值点长度的平方根累加的值\(\sum_{j=1}^{i}\sqrt{|F_{j-1}F_j|}\)，通常情况下，这个方法的效果要好于弦长累加法，尤其是在节点分布不均匀的情况下。
3. 统一节点法：顾名思义，每个节点的间隔都是相等的。这种方法不怎么在实践中获得应用。

在AutoCAD中，绘制样条线(输入SPLINE命令)，可以选择的节点参数化类型为上述三种，默认的是弦长累加法。

autocad 节点参数化

本节中，我使用的算法是累加弦长法，当然，你也可以替换成其他任意的参数化方法。参数的问题搞定了，需要考虑的第二个问题就是，我们选择插值的样条曲线的阶次。

2)选择阶次

B-Spline的三个要素是 节点(序列)、阶次、控制点。阶次由我们确定。样条曲线的性质是n阶B样条在节点处有n-1阶连续性，一般工业上常用的连续性到\(C^2\)，所以常用的曲线是3阶(cubic)曲线。AutoCAD默认的样条曲线阶次也是三阶。我也选择p=3阶。曲线的阶次确定了，节点确定了，就可以推出曲线的节点序列(knot vector)是(我们要插值的是“clamped b spline”):$$\{0,0,0,0,u_1,\cdots,u_i,\cdots,u_x,u_x,u_x,u_x\}$$而且，我们可以给出每个节点对应的基函数的值。因此，最开始的矩阵的左边就解决了。那么，左边的矩阵N已知，右边的型值点F已知，是不是可以通过解方程了求出最终的未知数控制点向量P了？

不是的:(。因为上面的方程其实是一个欠定方程(underdetermined equation)。简单的说，就是方程的数量小于未知数的数量。因为：在样条曲线的性质中节点、阶次、控制点的个数关系是\(n=m-p-1\)，现在我们的节点数是：x+1+6=x+7个，那么可以算出对应的控制点个数是m-4=x+3个，比我们已知条件x+1个型值点恰好多了两个。所以上面方程是没有唯一解的。怎么办？可以通过增加“边界条件”增加方程的个数。这里，我们需要至少两个边界条件。

3）边界条件(end conditions)

首先，边界条件可以根据实际情况任意指定。其次，边界条件不一定只要两个，而是至少两个。但是多与两个的情况下，你的方程将变为“超定方程”，需要采用类似最小二乘法等方式进行“折中”。一般来说，最常用或者说最实用的边界条件通常是两条：曲线在首尾点的切矢量。比如AutoCAD就是这么规定的。

为什么在Auto绘制的时候，默认的切矢量是0呢(如上图)？，因为AutoCAD可以根据用户输入的型值点推导出曲线端点的切矢量，因此，当切矢量不作为用户输入时，AutoCAD不显示切矢量的值。常用的切矢量推导算法是”Bessel Tangents“。再结合B样条的求导，可以知道首尾处的导数为$$ \left\{
\begin{aligned}
C^\prime(0) & = \frac{p}{u_{p+1}-u_1}(P_1-P_0); \\
C^\prime(u_x) & = \frac{p}{u_{p+n}-u_n}(P_n-P_{n-1});(n=x+2)
\end{aligned}
\right.
$$改成矩阵形式：$$\begin{bmatrix}
-1&1&0&\cdots&0\\
0&\cdots&0&-1&1
\end{bmatrix}
\begin{bmatrix}
P0\\P1\\\cdots\\P_{n-1}\\P_n
\end{bmatrix}=
\begin{bmatrix}
C^\prime(0)\frac{u_{p+1}-u_1}{p} \\
C^\prime(u_x)\frac{u_{p+n}-u_n}{p}
\end{bmatrix}
$$将这两条追加到最开始的方程中，方程就可解了。

4）我的C++实现

//Eigen 
#include <Dense>
/*!
 *\brief 三次B样条插值
*\ param const std::vector<Point> & vecFitPoints待插值点集合，需要点数不小于3
*\ Returns:   BSpline 插值样条曲线
*/
BSpline BSpline::CubicInterpolate(const std::vector<Point>& vecFitPoints)
{	
	const int p=3;
	BSpline bs;
	int x = vecFitPoints.size();
	if(x<p)
	{
		cout<<"too less point !"<<endl;
		return bs;
	}

	//求解方程 N*P = F
	Eigen::MatrixXd N= Eigen::MatrixXd::Zero(x+2,x+2);
	Eigen::MatrixXd P= Eigen::MatrixXd::Zero(x+2,3);
	Eigen::MatrixXd F= Eigen::MatrixXd::Zero(x+2,3);
	
	bs.m_nDegree = p;
	bs.m_vecKnots.resize(x); //x+6个节点
	//计算节点
	bs.m_vecKnots[0] =0.0;
	for (int i=1;i<x;++i)
	{
		bs.m_vecKnots[i] = bs.m_vecKnots[i-1] 
		+ PointDistance(vecFitPoints[i],vecFitPoints[i-1]);
	}
	//节点首尾构成p+1度重复
	bs.m_vecKnots.insert(bs.m_vecKnots.begin(),p,bs.m_vecKnots.front());
	bs.m_vecKnots.insert(bs.m_vecKnots.end(),p,bs.m_vecKnots.back());

	//1.填写矩阵N
	std::vector<double> basis_func;
	N(0,0) = 1;
	N(x-1,x+1) = 1;
	for (int i=p+1;i<x+p-1;++i)
	{
		//c(u)在 N_{i-p},...,N_i等p+1个基函数上非零
		bs.BasisFunc(bs.m_vecKnots[i],i,basis_func);
		for (int j=i-p,k=0;j<=i;++j,++k)
		{
			N(i-p,j) = basis_func[k];
		}
	}
	
	//导数
	N(x,0) = -1;
	N(x,1) = 1;
	N(x+1,x) = -1;
	N(x+1,x+1) = 1;

	//2.填写矩阵F
	for (int i=0;i<x;++i)
	{
		F(i,0) = vecFitPoints[i].x;
		F(i,1) = vecFitPoints[i].y;
		F(i,2) = vecFitPoints[i].z;
	}
	
	{
		Vec3d v0,v1,v2;
		BesselTanget(vecFitPoints[0],vecFitPoints[1],vecFitPoints[2],v0,v1,v2);
		Vec3d v= v0*(bs.m_vecKnots[p+1]-bs.m_vecKnots[1])/(double)p;
		F(x,0) = v.x;
		F(x,1) = v.y;
		F(x,2) = v.z;
	}
	
	{
		Vec3d v0,v1,v2;
		BesselTanget(vecFitPoints[x-3],vecFitPoints[x-2],vecFitPoints[x-1],v0,v1,v2);
		Vec3d v= v2*(bs.m_vecKnots[x+1+p]-bs.m_vecKnots[x+1])/(double)p;
		F(x+1,0) = v.x;
		F(x+1,1) = v.y;
		F(x+1,2) = v.z;
	}

	//解方程 N*P = F
	P = 	N.lu().solve(F);

#ifdef _DEBUG
	cout<<"N--------------"<<endl<<N<<endl;
	cout<<"F--------------"<<endl<<F<<endl;
	cout<<"P--------------"<<endl<<P<<endl;
#endif

	//将Eigen所求的结果赋给bs的control_vertex
	bs.m_vecCVs.resize(x+2);
	for(int i=0;i<x+2;++i)
	{
		Point& cv = bs.m_vecCVs[i];
		cv.x = P(i,0);
		cv.y = P(i,1);
		cv.z = P(i,2);
	}
	
	return bs;
}

5)与AutoCAD的对比

下图是我的插值结果(红色线)与AutoCAD “SPLINE”工具插值生成的样条曲线(白色线)的对比。可以看到，我的插值结果与AutoCAD结果的不同之处在于曲线的首末端点的导数估计上。其他的比如度数，控制点个数、参数化方法均相同。可见，AutoCAD对于端点导数的估计算法应该不是“Bessel Tangent”法。

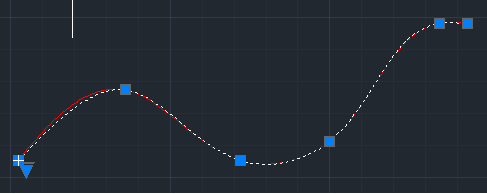
我的B样条插值结果(红色)与AutoCAD插值算法(白色)比较，二者的端点导数估计算法不一样

参考资料

The Essentials of CAGD : Chapter 11 Working with B Spline Curves