与Bezier曲线的打断方法类似，B样条的打断利用了de Boor算法。并且结合B样条的强凸包性，我们可以推算出一种有效的B样条折线化方法。因此，本节是对前面几节内容的一个综合应用，后面，我的分享也主要面向应用。
1）B样条的打断
给定参数u,希望在u处将b样条分为两部分。这个过程与Bezier曲线的打断非常相似。只不过，Bezier的打断是在所有的控制点上进行“切角”，而对于\(u\in[u_k,u_{k+1})\)，仅\(P_{k-p},…,P_k\)p+1个控制点被切角(其实Bezier曲线也是p+1个控制点…)。下图以三阶B样条为例，展示打断过程：
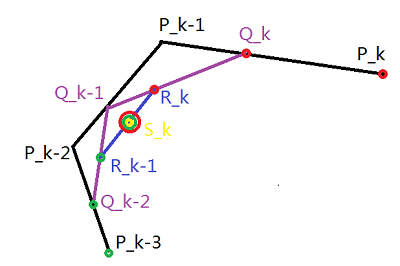
我分别用Q,R,S代表三次“切角”。de Boor算法最后计算出的C(u)即\(S_k\)。绿色的点\(P_{k-3},Q_{k-2},R_{k-1},S_{k}\)为打断后左边的B样条的新控制点，\(S_{k},R_{k},Q_{k},P_{k}\)为打断后右侧的B样条的新控制点。
我的C++版本的打断实现如下：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
void BSpline::Subdeviding(double u,BSpline& sub_left,BSpline& sub_right) { //为了使用方便 const std::vector<double>& knots = m_vecKnots; const std::vector<Point>& cv = m_vecCVs; int p = m_nDegree; //查找 u 所在区间 int k = std::distance(knots.begin(),std::upper_bound(knots.begin(), knots.end(), u))-1; //保存de boor 算法迭代过程中生成的控制点 std::vector<Point> cv_left,cv_right; _subdeviding(u,k,knots,cv,cv_left,cv_right); //曲线在u处打断，生成新的控制点序列 假设原曲线的控制点序列为 P_0,...,P_k-p-1,P_k-p,...,P_k,P_k+1,...,P_n //打断后的新控制点序列为：左侧：P_0,....,P_k-p-1,cv_left[...]，右侧 cv_right[...],P_k+1,...,P_n。 //sub_left sub_left.m_nDegree = p; //knots sub_left.m_vecKnots.resize(k+p+2); for (int i=0;i<k+1;++i) sub_left.m_vecKnots[i] = knots[i]; for (int i=0,j=k+1;i<p+1;++i,++j) sub_left.m_vecKnots[j] = u; //control vertex sub_left.m_vecCVs.resize(k+1); for (int i=0;i<k-p;++i) sub_left.m_vecCVs[i] = cv[i]; for (int i=0,j=k-p;i<p+1;++i,++j) sub_left.m_vecCVs[j] = cv_left[i]; //sub_right sub_right.m_nDegree = p; //knots sub_right.m_vecKnots.resize(knots.size()-k+p); for (int i=0;i<p+1;i++) sub_right.m_vecKnots[i] =u; for (int i=p+1,j=k+1;j<knots.size();++j,++i) sub_right.m_vecKnots[i]=knots[j]; //control_vertex sub_right.m_vecCVs.resize(cv.size()-k+p); for (int i=0;i<p+1;++i) sub_right.m_vecCVs[i] = cv_right[i]; for (int i=k+1,j=p+1;i<cv.size();++i,++j) sub_right.m_vecCVs[j] = cv[i]; } void BSpline::_subdeviding(double u,int k,const std::vector<double>& knots,const std::vector<Point>& cv, std::vector<Point>& cv_left,std::vector<Point>& cv_right) { int p= m_nDegree; //保存de boor 算法迭代过程中生成的控制点 cv_left.resize(p+1); cv_right.resize(p+1); //将 P_k-p,...,P_k拷贝到cv_left上面 std::copy(cv.begin() + k - p, cv.begin() + k + 1, cv_left.begin()); cv_right[p] = cv_left[p]; //de-boor 迭代p次 for (int r = 1; r <= p; ++r) { //i 从 k 到 k-p+1 for (int i = k,j=p; i >= k - p + r; --i,--j) { double alpha = u - knots[i]; double dev = (knots[i + p + 1 - r] - knots[i]); alpha = (dev !=0)? alpha/dev : 0; cv_left[j] = (1.0 - alpha)*cv_left[j - 1] + alpha * cv_left[j]; } cv_right[p-r] = cv_left[p]; } } |
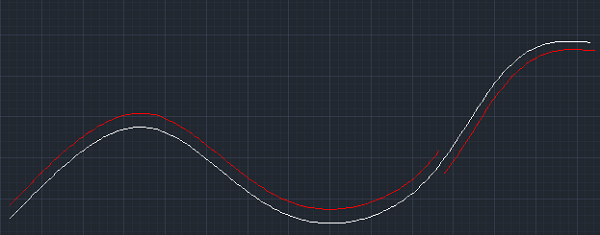
下图是打断算法对某一样条在\(u=3000\)处打断的效果。为了方便展示，两段打断后的样条曲线都经过了移动。
2）B样条的折线化
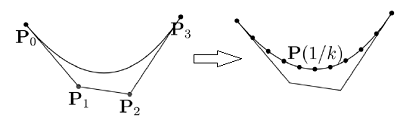
B样条的折线化也是最常用的功能之一。比如曲线转换成折线，曲线渲染等等都需要将用一系列离散点代表B样条曲线。因此也可以把这个过程称之为曲线的细分(Tesselation)。一种简单的(naive)想法是均匀细分，即将节点区间均匀的划分为k份，然后对新节点分别求值，算出曲线上的点代替原曲线。如下图示：
这种划分比较简单，但是缺点也比较明显，即参数的步长不好确定。步长过大对于弯曲的曲线容易造成折线折角过大，步长过小会造成数据冗余。因此，我们需要一个自适应的方法。回想B样条的一个性质是“强凸包性”，说的是B样条曲线严格包含在控制点构成的凸包之内。因此，我们可以通过凸包的形状预测曲线的形状。当凸包形状逼近直线时，曲线的形状也逼近直线。自适应算法采用“分而治之”的思路，递归的将曲线分成两部分做细分运算：
- 给定节点首尾 \(u_{beg},u_{end}\),计算所有控制点到首、尾控制点的最高高度，如果最高高度小于阈值d，那么曲线足够直，计算终止，输出折线化结果。
- 如果不满足阈值，将曲线在 \(u_{mid}=(u_{beg}+u_{end})/2\)处打断，分成两部分，并且分别将两个部分执行步骤1。
我的算法的C++的实现是：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
void BSpline::Tesselation(double tolerance ,std::vector<Point>& points) { std::vector<Point> cv_copy = m_vecCVs; std::vector<double> knots_copy = m_vecKnots; _tesselation(cv_copy, knots_copy, points, tolerance, m_nDegree, m_vecKnots.size() - m_nDegree,0,m_vecCVs.size()-1); } void BSpline::_tesselation(std::vector<Point>& cv, std::vector<double>& knots, std::vector<Point>& points, double tolerance, int k_s, int k_e,int c_s,int c_e) { int p = m_nDegree; bool stright_enough = true; //计算弦高是否超过容差 for (int i = c_s + 1; i < c_e; ++i) { //点到直线距离公式，不给出实现了 if (PointLineDistance(cv[i], cv[c_s], cv[c_e]) > tolerance) { stright_enough = false; break; } } //满足要求，不进一步细分了 if (stright_enough) { //为了保证控制点不重复，设计的规则为[),但是对最后一个点例外。 //按照递归顺序，最后一段首先加入points int c_end = points.empty() ? c_e +1: c_e; points.insert(points.begin(),cv.begin()+c_s,cv.begin()+c_end); return; } //从节点中间打断 double u_mid = knots[k_s] + (knots[k_e] - knots[k_s]) / 2.0; //查找 u 所在区间 int k = std::distance( knots.begin(),std::upper_bound(knots.begin(), knots.end(), u_mid)) - 1; std::vector<Point> cv_left, cv_right; _subdeviding(u_mid,k,knots,cv,cv_left,cv_right); //节点区间新增p个u_mid knots.insert(knots.begin() + k+1, p,u_mid); //控制点替换 cv.insert(cv.begin() + k, p,Point()); for (int i = k - p, j = 0; j <p; ++j, ++i) cv[i] = cv_left[j]; for (int i = k, j = 0; j <= p; ++j, ++i) cv[i] = cv_right[j]; //两部分分别递归 //Note:后半部分在前半部分之前执行， //因为如果前半部分首先执行的化，后半部分的索引就发生改变了 _tesselation(cv, knots, points, tolerance, k + 1, k_e + p,k,c_e+p); _tesselation(cv, knots, points, tolerance, k_s, k + 1, c_s, k); } |
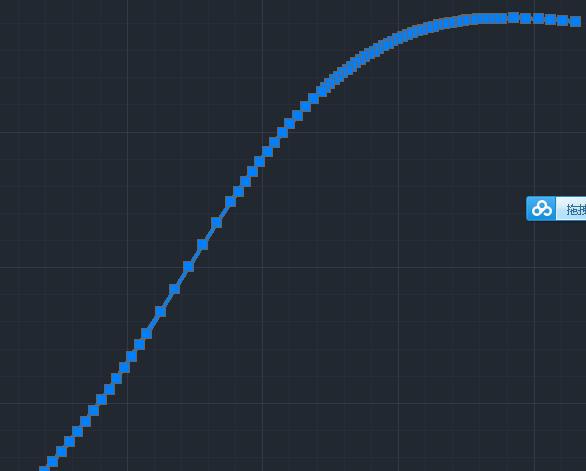
下图是对某条3阶B样条曲线进行torlerance =1 的折线化局部效果，可以看到：折线在弯曲的地方点比较密，而平直的地方点比较少，所以具备较好的自适应的特点。
3）折线化算法分析：
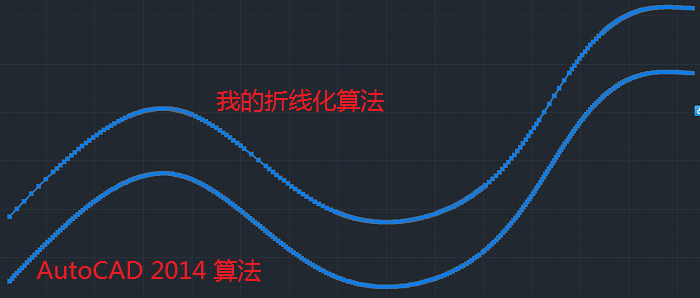
上述的算法与AutoCAD 样条曲线“转换为多段线”功能的对比：同样一段样条曲线，在AutoCAD中，AutoCAD的样条曲线“转换为多段线”功能转出的多段线相对来说更加均匀，可能没有考虑到“自适应”问题。如下图，我使用AutoCAD“转换为多段线”功能与我计算的多段线在近似效果相近的程度下进行比较（AutoCAD使用0-99的相对精度，我使用“弦高”的概念，二者无法直接对照。AutoCAD使用精度90，我使用容差1，目测二者差别接近），我的效果是254个点，AutoCAD是267个点。
本文参考： Dartmouth College 某个关于样条曲线的ppt给出了大体的思想，但是网页链接找不到了。
大佬，能不能发一下完整版的代码。
请问NURBS曲线怎么打断呢