在基函数的性质中我们已经学习过，B样条基函数\(N_{i,p}\)的作用范围是局部的，因此与Bezier曲线不同，移动控制点\(N_{i,p}\)对B样条的影响是局部的。而且，通过基函数“强凸包性”的特点，我们可以推导出若干样条曲线修型的技巧。

移动控制点

B样条曲线的矩阵形式如下：$$C(u) = \begin{bmatrix}N_0&N_1& \cdots &N_n\end{bmatrix}\begin{bmatrix}P_0\\P_1\\ \cdots \\ P_n\end{bmatrix}$$如果将\(P_i\)移动到\(P_i+\vec v\),新曲线\(D(u)\)的定义是：$$D(u) = \begin{bmatrix}N_0& \cdots &N_i& \cdots &N_n\end{bmatrix}\begin{bmatrix}P_0\\\cdots \\P_i+\vec v\\ \cdots \\ P_n\end{bmatrix} = C(u) + N_i\vec v$$即新曲线为原曲线整体移动\(N_i\vec v\)。

因为基函数\(N_i\)仅在区间\([u_i,u_{i+p+1})\)上非0，所以控制点\(P_i\)的移动仅对这段区间内的曲线起作用。而且，因为\(0<N_i \le 1\)，所以可知曲线的移动与\(\vec v\)同向，并且距离不超过\(|v|\)。

修型技巧

基函数的“强凸包性”指的是曲线上\(u_i,u_{i+1}\)段一定在由控制点\(P_{i-p},…,P_i\)构成的凸包之中。因此，我们可以通过控制凸包的形状影响曲线的形状。下面的技巧，大家都可以下载 Nurbs demo 自行实践。

1）令 \(P_{i-p},…,P_i\)共线，使得曲线\(u_i,u_{i+1}\)段成为直线。因为凸包变成直线，凸包内的曲线自然被“压扁”为直线。

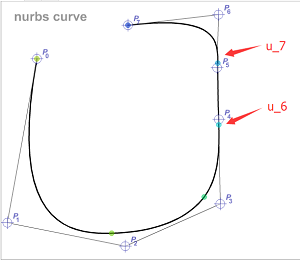
如上图，通过使\(P_3,…,P_6\)共线，可以使得曲线段\([u_6,u_7)\)与控制点共线。

2）令\(P_{i-p+1},…,P_{i}\)共p个点重合，曲线段使得曲线\(u_i,u_{i+1}\)段成为直线，并且曲线通过控制点\(P_i\)。如下图。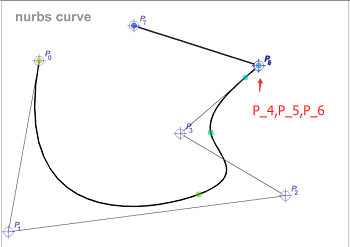

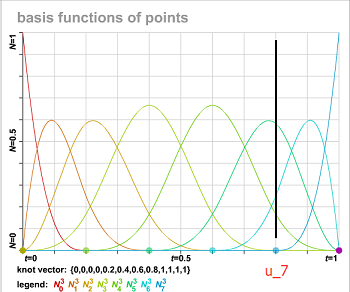
首先控制点构成直线，曲线变成直线。当\(u=u_7\)时，\(N_3=0\),\(N_4+N_5+N_6=1\)，而且后p个控制点重合，使得\(C(u_7)=P_6\)。

3） 令\(P_{i-p+1},…,P_{i}\)共p个点重合，且\(P_{i-p},P_i,P_{i+1}\)共线,曲线与三点所构成的直线相切。这一条是对第二条的扩展。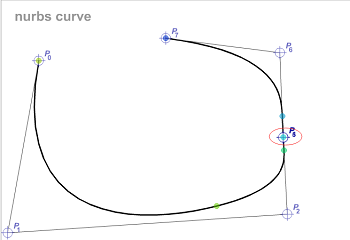

如图，\(P_2,P_3=P_4=P_5,P_6\)共线，曲线与控制多边形\(P_2,P_6\)相切。

本节参考 Introduction to Computing with Geometry 6.3.4节。