与Bezier曲线一样，B样条对于给定参数u求曲线上点的算法都不是通过计算基函数的值后带入控制点坐标计算的，而是通过de Boor算法计算，但是在曲线内插、拟合、优化等后续话题中，都需要带入基函数的值。因此本节的目标是介绍给定任意参数u,计算一组\(N_{i,p}(u)\)值的算法。

原始方法(naive method)

首先，回想B样条基函数的递归公式：$$ N_{i,0}=\left\{\begin{aligned}1&  & u \in [u_i,u_{i+1}) \\0 &  & otherwise \end{aligned}\right. \\ N_{i,p}(u)=\frac{u-u_i}{u_{i+p}-u_i}N_{i,p-1}(u) + \frac{u_{i+p+1}-u}{u_{i+p+1-u_{i+1}}}N_{i+1,p-1}(u)$$通过这个公式，我们可以计算任何\(u\in[u_0,u_m)\)所对应的一组基函数值\([N_{0,p}(u)],[N_{1,p}(u)],…,[N_{n,p}(u)]\)。但是，通过基函数的性质我们也了解到，在这n+1个基函数里面，至多也只有p+1个基函数有值呢。如果按照上述迭代式，我们会浪费n-p个基函数的运算，因为他们的值根本就是0。而且，如果按照递归方式实现上述计算过程，那么还会造成另外一种浪费：如同de Casteljau’s 与Fabonacci算法的递归实现一样，很多参数一样的函数被多次重复执行了。

改进方式

因为大部分应用中的B样条都是“clamped B-Spline”即前p+1个与后p+1个节点重复的样条，因此我们可以假定参数u位于节点区间\([u_p,u_{m-p}]\)。

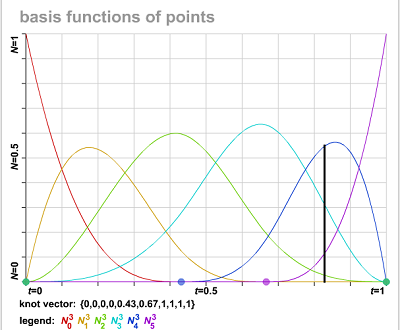
而且，观察上图的基函数曲线，可以知道当\(u\le u_p\)时，\(N_0=1\),其他基函数为0。当\(u\ge u_{m-p}\)时，\(N_n=1\),其他基函数为0。

对于\(u\in (u_p,u_{m-p})\)，有如下办法：

1. 对于\(u\in [u_k,u_{k+1})\)，至多\(N_{k-p},…,N_k\)等p+1个基函数非0。
2. \(N_{k-p},…,N_k\)在区间 \([u_{k-p},u_{k+p+1})\)上非0。
3. 在区间 \([u_{k-p},u_{k+p+1})\)上,\(N_{k,0}=1\)，其他\(N_{i,0}=0\)。

可以看到\(N_{i,0}\)数组共2p+1个值已经给出，可以按照递推公式算出\(N_{i,1}\)共2p个，迭代p次后得到p+1个值即\(N_{k-p},…,N_k\)。

我的算法C++实现如下：

/*!
*\brief b样条曲线基函数计算
*\ param double u 参数值
*\ param int k 区间 k。可以通过std::upper_bound()-1获得
*\ param std::vector<double> & basis_func basis_func基函数值，对应N_{k-p},...,N_k
*\ Returns:   void 
*/
void BSpline::BasisFunc(double u,int k,std::vector<double>& basis_func)
{
	const int& p = m_nDegree;
	const std::vector<double>& knots = m_vecKnots;
	basis_func.resize(p+1);

	//2p+1个 N_{i,0}
	int n = 2 * p + 1;
	vector<double> temp(n,0);
	temp[p] =1;

	//迭代p次
	for (int j=1;j<=p;++j)
	{
		//区间 [k-p,k+p+1)
		for (int i=k-p,h = 0;h < (n - j);++h,++i)
		{
			//递推公式
			double a = (u - knots[i]);
			double dev = (knots[i+j] - knots[i]);
			a = (dev !=0) ? a /dev : 0;

			double b = (knots[i+j+1]-u);
			dev = (knots[i+j+1] - knots[i+1]);
			b = (dev != 0)? b/dev : 0;
			
			temp[h] = a*temp[h] + b*temp[h + 1];
		}
	}
	//拷贝前 p+1个值到basis_func
	std::copy(temp.begin(), temp.begin() + p + 1, basis_func.begin());
}