本节的目标为介绍B样条曲线的定义，以及其重要性质。这些性质，对样条曲线的应用起了决定性的作用。

1.定义: 

与Bezier曲线的定义相似，B样条曲线的定义是：给定n+1个控制点\(\{P_0,P_1,…,P_n\}\),m+1个节点\(\{u_0,u_1,…,u_m\}\),p阶B样条曲线\(C(u)=\sum_{i=0}^n N_{i,p}(u)P_i\)。相对Bezier曲线不同之处在于：

1. B样条 的控制点个数与曲线次数无关，因此B样条的自由度更大，可以定义很多控制点又不用担心曲线次数过高而计算困难。
2. B样条有多个节点区间，使得其为分段函数，而Bezier曲线只有一个区间。

二者的联系是：

1. B样条上任意一个区间\([u_i,u_{i+1})\)上的曲线的定义都是一个Bezier。因此可以将B样条转为分段bezier曲线。
2. Bezier是一种特殊的样条曲线。后面会详细分析。

2.性质

因为是bezier曲线的一般形式，B样条曲线的很多性质都和bezier曲线相同。而且，B样条有很多更好的性质。一条由n+1个控制点，m+1个节点，p次(m=n+p+1)的B样条曲线有如下性质：

1. B样条上任意一个区间\([u_i,u_{i+1})\)上的曲线的定义都是一个Bezier曲线。相对于bezier曲线，B样条曲线能够更好的控制曲线形状。如下图，左侧是11个控制点构成的3次样条曲线，右侧是同样控制点构成的10次Bezier曲线，其曲线可控制性要比样条曲线差。如果定义一样的控制点，阶次越低，曲线离控制点就越远。当然了，如果曲线的阶次为1，那么曲线就是控制多边形本身==!。
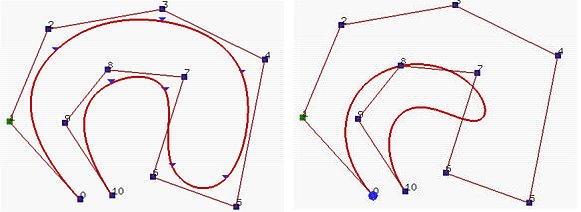
2. m,n,p必须要满足的关系是m=n+p+1。这个在基函数的定义里面就证明了。
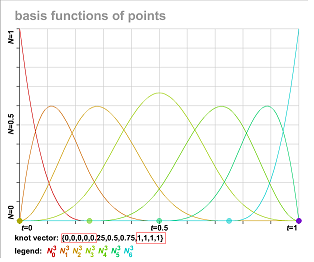
3. “clamped”B样条（如上图左），就是首尾节点重复度分别为p+1的样条，曲线的首尾点分别和首尾控制点相同。这个和bezier曲线一样。如何证明呢？可以将u=0带入de-Boor迭代式中求解，只不过，因为重复节点(0长度区间)的存在，我们需要定义\(\frac{0}{0}=0\)。实际上，可以通过上节我介绍的swf文件直接观察B样条基函数的情况。如下图，\(N_0,N_6\)在节点区间首末点处均为1，其他基函数为0，那么带入B样条，可以得出\(C(0)=P_0;C(1)=P_6\)。
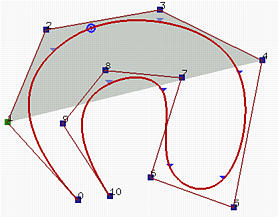
4. 强凸包性:对应区间\([u_i,u_{i+1})\)上曲线一定在由p+1个控制点\(P_{i-p},…,P{i}\)构成的凸包之中。因为在这段区间上，\(N_{i-p},…,N{i}\)是大于0的（原文为非0），而且根据基函数的性质，几者相加等于1，那么中间的曲线相当于这几个点的“加权平均”，自然位于其凸包之内。所谓强凸包性，指的是曲线要比凸包要小的多。这个性质在曲线的折线化（离散）时非常有用。如果我们能让控制点构成直线，那么对应的曲线也能形成直线。
5. 局部修改模式：修改控制点\(P_i\)，那么其影响的曲线范围仅限于区间\([u_i,u_{i+p+1}\)。对应的是基函数的非零范围。因此，大家可以记住，\(N_i\)与\(P_i\)是一对，如果\(N_i\)非零，那么\(P_i\)的变化就会对对应区间产生影响。在实际生产中，用户通常通过加入节点，增加节点个数的方式获取更多的控制点，进而利用B样条的局部修改模式细化调整曲线，而不影响曲线整体走势。
6. 样条曲线在节点处的连续性为\(C^p\)，在重复度为k的节点处的连续性为\(C^{p-k}\)。普通节点的重复度为1。因为\(C^2\)已经能够保证曲率连续了，所以在一般的业务应用中，三次(cubic)样条曲线最为常用。
7. 变差减少性(Variation Diminishing Property)：这条性质与Beizier曲线的相近，如果一条直线与样条曲线的控制多边形的交点数为N,那么这条直线与样条曲线的交点数应该不大于N。
8. Bezier曲线是特殊的样条曲线。因为Bezier曲线的控制点个数为次数+1，所以，当将样条曲线的控制点取p+1个，节点序列取\(\{0,0,…,0,1,1,…1\}\)曲线即为bezier曲线。
9. 仿射不变性：这一条的意思是，如果需要对样条曲线做变换，那么只需要对其控制点序列做变换就可以了。其参数区间，次数保持不变。非常好的性质。
   

   ---

   补充，当\(u=u_i\)时，\(N_i=0\)。而且对应区间上至多有p+1个非零基函数。因此性质第4条强凸包性应该是在区间\((u_i,u_{i+1})\)且p<i<m-p时成立。

B样条的优点：

如我在Nurbs历史中谈到的，B样条是对贝塞尔曲线的一般化。因而，Bezier曲线能表达的，B样条也同样可以。而且，因为B样条引入了控制点个数与曲线阶次无关的特性，使得我们可以对低阶曲线有了更好的控制能力。而且，通过对节点序列的控制，使得我们对曲线有自由的调节能力。”NURBS”代表的非均匀有理B样条，我们就差“有理”没有接触了。B样条仍然是多项式曲线，不能用来表达圆，圆锥曲线等有理曲线，所以NURBS是B样条的更一般化的形式，可以表达上述有理曲线。

本节参考：Introduction to Computing with Geometry  : B-Spline Definition & Important Properties