B样条的形式与Bezier曲线的定义方式相同:C(u) = \sum_{i=0}^n N_{i,n}(u)P_i 但是其基函数的形式有很大的变化。重要的一个不同是,B样条的基函数是定义在一组参数区间上的。这一节,我将介绍B样条的基函数。
令U为m+1个非递减的参数\{u_0\le u_1 \le … \le u_m\} 每个u_i叫做节点,U成为节点序列(Knot Vector),半闭半开区间[u_i,u_{i+1})称为第i个节点区间(knot span)。基函数的节点是允许存在重复的,如果u_i出现了k次(k>1),那么称其为k重节点。如果u_i仅出现一次,那么称其为简单节点。如果说所有的[u_i,u_{i+1})区间的长度都是一样的,那么称节点区间为均匀区间,反之称为非均匀区间。“非均匀有理B样条”就是说其节点区间为非均匀的。节点将区间[u_0,u_{m}]分成多段。但是考虑N_{i,p}(u)时,可以认为其定义域是在[u_0,u_{m}]上的,但是其只在有限的区间上非0,因此,对比Bezier曲线的基函数,B样条的基函数是比较局部的。
B样条的基函数由三个参数决定:阶数p,参数u,第i个基函数。B样条的基函数由递归公式给出: N_{i,0}=\left\{\begin{aligned}1& & u \in [u_i,u_{i+1}) \\0 & & otherwise \end{aligned}\right. \\ N_{i,p}(u)=\frac{u-u_i}{u_{i+p}-u_i}N_{i,p-1}(u) + \frac{u_{i+p+1}-u}{u_{i+p+1-u_{i+1}}}N_{i+1,p-1}(u)
上述表达式被称为 Cox-de Boor 迭代式。这个式子看起来比较复杂,实则不难理解。为了理解方便,我们可以以5阶B样条的基函数为例,看一下N_{0,5}的计算
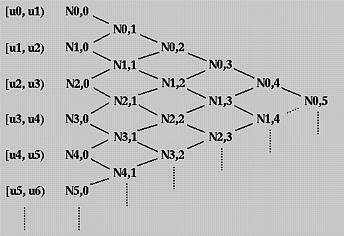
N_{0,5}为N_{0,4},N_{1,4}的线性组合,N_{0,4},N_{1,4}又分别是N_{0,3},N_{1,3},N_{2,3}的线性组合……经过五次迭代后,可以得出N_{0,5}为5次多项式,而且其在区间[u_0,u_6)上非0。
下图可以分析上述线性组合系数的含义。
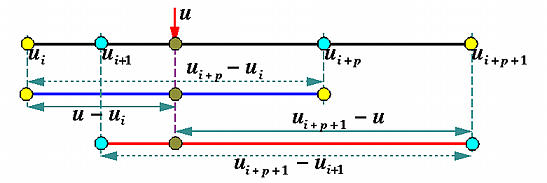
根据deBoor迭代式,N_{i,p}由N_{i,p-1},N_{i+1,p-1}组合而成。N_{i,p-1}在区间[u_i,u_{i+p})上非零。N_{i+1,p-1}在区间[u_{i+1},u_{i+p+1})上非零。可以分情况讨论
- 当u\in [u_i,u_{i+1})时,N_{i+1,p-1}=0,N_{i,p}仅由N_{i,p-1}决定。系数为uu_i占u_iu_{i+p}(蓝线)的比例。
- 当 u\in[u_{i+p},u_{i+p+1})时,N_{i,p-1}=0,N_{i,p}仅由N_{i+1,p-1}决定。系数为uu_{i+p+1}占u_{i+1}u_{i+p+1}(红线)的比例。
- 当 u\in[u_{i+1},u_{i+p})时,两项都不为零,N_{i,p}为二者的线性组合,系数与上述相同。
基函数的性质
为了讨论基函数的性质,我有必要先贴出一个nurbs基函数的flash的链接,大家可以下载后设置打开方式为chrome/firefox/IE自行浏览。
http://geometrie.foretnik.net/files/NURBS-en.swf
这个动画非常直观的表现了基函数的所有性质,需要认真的实验即便细细体会。
- n阶B样条的基函数为n次多项式。N_{0,5}的图里可以看到。
- 非负性。所有的N_{i,p} \ge 0。如下图,可以看到所有的曲线都位于坐标轴上方。
- 局部性。对N_{0,5}的观察推而广之,可以得出N_{i,p}在区间[u_i,u_{i+p+1})上非零。结合下图,可以看到每个基函数仅在有限个区间上非零。
- 反过来看,在区间[u_i,u_{i+1})上,非零的基函数非别为 N_{i-p},…,N_i共p+1个。当然,通过i-p \ge 0得出,当i <p时,非零基函数小于p+1个。因此在区间[u_i,u_{i+1})上,非零基函数至多为p+1个。结合下图中的黑线,可以看到在0.5与1.0间随便取一个参数u,其对应曲线有4个非零值。
- 单位分解率。在区间[u_i,u_{i+1})上,非零基函数 N_{i-p},…,N_i的和为1。这一点与bezier曲线的基函数性质相同(当然了,bezier曲线只是B样条的一个子集)。
- 如果节点的数量为m+1个,控制点的个数为n+1个,则存在等式m=n+p+1。因为最后一个基函数N_{n,p}在区间[u_n,u_{n+p+1})上非零。所以说u_{n+p+1}=u_m为最后一个节点。这个等式,我们后面会经常用来确定节点与控制点的个数关系。
- 基函数在其非零区间中是由多段多项式函数组合而成的。实际上,在每个节点区间上,基函数拥有独立的多项式系数。
- 如果一个节点u的重复度为k,那么任意基函数在u处的连续性为C^{n-k}。
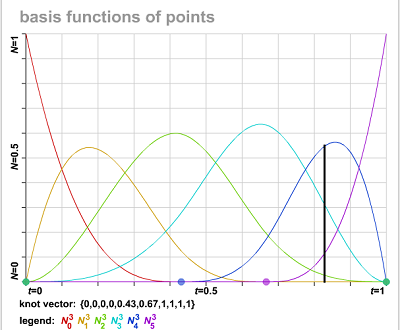
基函数的性质说明
节点多重性的影响
当学到调整节点区间时,我们将会看到通过制造多重节点带来的特殊效果。这里,我的角度与Dr.Shene有点不同,我们暂时可以认为多重节点在基函数方面没有表现出特殊的性质,即:长度为0的区间也是有效的区间。
