了解完一种特殊的nurbs曲线：贝塞尔曲线后,从本节开始，我将逐步介绍非均匀有理本样条曲线。理解bezier曲线的相关概念对NURBS的学习非常有帮助。本文的目标是介绍NURBS曲线的背景、主要应用和基本概念,并且介绍NURBS的前世今生。

1.动机

Bezier曲线在生产实践中如果需要构造复杂图形，通常需要多条曲线连接。因为bezier曲线的阶数与控制点数量是对应的，所以单条曲线如果要更大的自由度必须提高阶数，给计算效率和数值稳定带来问题。但是如果要维持bezier曲线在接头处的连续性也比较无聊，给设计工作带来复杂性。更重要的是，如果说维持\(G^1\)条件比较简单的话，维持更高次数的连续性就更加复杂了。有没有一种能够承载更多控制点(自由度)，更低的阶数的参数曲线呢？答案就是NURBS，或者说样条曲线。

考虑到章节安排，我们先讨论NURBS的无理形式B样条，然后在扩展到有理形式。后面你会看到，二者的转换非常方便。

2.什么是NURBS曲线

简单的来说，NURBS即在一组(多个)区间上分别定义的bezier曲线。概念上相当于（其实就是）我们接触过的分段定义函数。他的特殊之处在于，用户不需要维护分段之间的连续性，n阶nurb天然拥有直到\(C^{n-1}\)级的连续性。因此，它就非常的强大了，允许我们在比较低的阶次下做出复杂的图形。

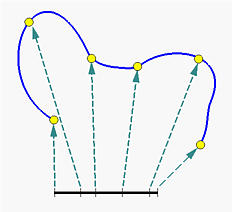
如上图，nurbs曲线对参数定义域进行了分割，假设对应的黄点处的参数只分别为\(\{u_0,u_1,u_2,u_3,u_4,u_5\}\)。这六个点将曲线分割为5部分，每个部分为一个bezier曲线。这些分割的参数成为曲线的节点(knot)。因此我们看到，相比于beizer仅有一个区间,nurb的参数定义域存在多个区间。nurbs有四个要素：

1. 阶数
2. 控制点序列
3. 节点序列
4. 控制点权值序列（仅存在于有理情况，这里不讨论）

打开AUTOCAD，输入spline 命令，画一段样条曲线，选中，输入ch命令，可以看到

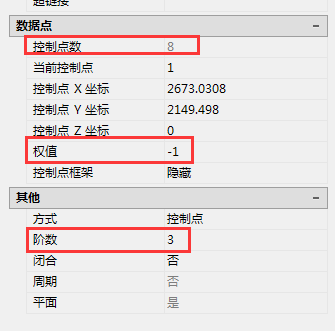
控制点个数为8个，阶数为3，当前控制点的权重为-1，代表的是Autocad的默认权值，表明当前曲线为无理曲线。节点序列在Autocad的用户界面中没有进行体现，一般在曲线构造时参数化方式的选择时确定。Autocad 共提供三种参数化方式，我们到后面会集中了解。

3.NURBS曲线的用途

1. NURBS是几何设计的工业标准。业界青睐NURBS的主要原因有：
2. 无论对于解析型曲线（圆、圆锥曲线等）还是自由构型曲线，都有统一的数学表达形式。
3. 自由度高，可以采用NURBS设计非常复杂的几何形体。
4. NURBS涉及的算法可以方便的在计算机上实现，而且执行效率和数值稳定性都很高。
5. 涵盖整个曲线族，是b样条曲线、bezier曲线的更一般形式。
6. 具有仿射变换和透视变换下的不变性，对图形处理非常友好。
7. 呈现曲线所需要的数据量比常规的polyline要小的多。
8. 广泛的用户群体，以及在大学教育中的普及性。

4.nurbs历史

人们对于样条的使用始于对流线型的追求。18世纪，船舶制造业从手工业发展为科学，船舶设计从手工模型作业转为图纸设计，为了保证船壳具有流线形状，并且平均分担行船过程中水的阻力，船舶设计者使用细小的有弹性的木条或者钢片，通过配重的钩子(“duck”)约束木条的形状设计船壳。这样的木条被称之为样条（“spline”）。

现代CAD的起源要追踪到法国汽车制造商雪铁龙，雪铁龙在50年代中期推出的DS系列汽车开始使用风洞设计，将雪铁龙汽车设计带到“航天时代”,因而名声大噪。在汽车的设计过程中，汽车的模型需要在设计者与工程师的手中传递，而且50年代末，法国汽车产业采用模拟计算机连接机床制造零件。圆形，抛物线等形状容易输入，而自由曲线亦需要有统一的数学形式。摆在工程师面前的问题是，有没有一种统一的数学形式，可以将汽车几何造型表达出来？

雪铁龙的 Paul de Faget de Casteljau在1963年发明了de Casteljau（德卡斯特里奥）算法，通过这套算法可以计算出“曲线”上的点。他顿悟了与其定义一条以长度作为参数的曲线，不如定义一系列控制点，通过改变控制点的形状影响曲线形状。在当时，de Casteljau的做法无疑是最大的创新，起初也遭到了公司内部的质疑，但是这个年轻的数学家最终说服公司采纳他的算法，并且最终获得成功。雪铁龙严格要求对de Casteljau算法保密，直到8年之后de Casteljau的成果才得以发表。

尽管雪铁龙进行了严密的保密工作，其竞争对手雷诺公司还是了解到了de Casteljau的工作，并且对他的工作进行了深入的研究，尽管不是de Casteljau算法本身。1966年，雷诺公司的bezier和他的团队独立的重现了de Casteljau的研究成果，并且将“曲线”正式命名为“Bezier”曲线。与雪铁龙不同，雷诺允许贝塞尔发表他的研究成果。所以现在大家一般都了解贝塞尔，而de Casteljau在大众中就没有那么高的知名度了。

有意思的是，贝塞尔的工作最初也收到了管理层的嘲讽。“如果说你的方法那么好，美国人肯定早就发明了！”听起来是不是似曾相识？可见当时的法国汽车制造业还是非常“传统”的。当然，美国人也没有闲着，GM的学者Carl de Boor发明了de Boor算法，是一种计算B样条上点的方法。尽管B样条作为一种数学模型在20世纪40年代就已经存在，但是因为de Boor算法优越的数值稳定性，B样条才发挥了它巨大的应用潜力。

波音公司的探索。波音公司是CAGD的先驱。50年代就推出了自己的设计软件，但是直到10年后，物理的木质样条仍然被很多波音工程师在工作中使用。而且不同的部门采用不同的模型，bezier曲线，B样条曲线等同时存在，波音迫切需要制定一种统一的数学模型统一公司上下。于是成了一个委员会。这个委员会最终设计了一种数学模型，称之为非均匀有理B样条（NURBS）。统一了波音所有的需求。并且快速成为CAD数据交换的工业标准。

虽然在航空，汽车，航海上得以应用，但是NURBS在表达复杂自然形状方面会遭遇拓扑问题，NURBS很难表达复杂的拓扑。1994年，Pixar 公司出版了著名的《玩具总动员》其中的各种人物与道具都是由很多NURBS曲面拼接而成的。但是这种处理特别的费时费力，而且容易发生错误。因而到97年《棋逢对手》发布时，Pixar切换到了表面细分（subdivision surfaces）技术。

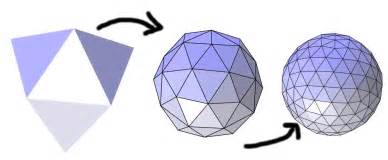
subdivision surfaces

从NURBS 转换到曲面细分，是设计与实现的分离。设计师仍然希望使用NURBS良好的控制特性，但是动画渲染人员更希望简单、容易计算的模型。纵观NURBS的发展，无非是数学模型不断一般化的过程，从开始的bezier,到B样条，再到无理B样条，再到NURBS，数学模型的泛化能力越来越强大。发展到现在，CAD领域最重要的任务之一就是建立细分表面(subdivision surfaces)之间的桥梁。

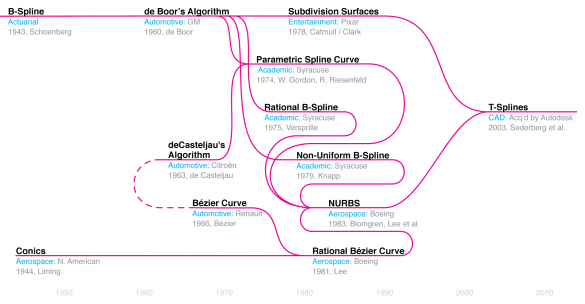
nurbs发展

最新的进展是T-Splines，由Autodesk引入,T-Splines 承诺将细分表面的逐步细化的接口、复杂的拓扑形状与NURBS曲面的精确性与控制力进行良好的融合，让用户具有更高的灵活性，而不需要考虑复杂的技术细节。

到这里，NURBS的发展历史基本上说完了。可以看到，nurbs从近代发展到今天，使命始终都是提供一种直观的数学模型和操作方式，解决人们在生产实践中的问题。伴随着计算能力的日益增长，AR/VR ,3D打印等技术的不断增强，开源软件规模的不断扩大，NURBS技术将会不断延伸到各个领域。

本文参考：

1. Introduction to Computing with Geometry 第六章第一节
2. 什么是NURBS?
3. About Nonuniform Rational B-Splines – NURBS
4. A Brief History of the Computational Curve