业务中使用曲线的目的，主要是因为曲线具有高阶导数连续的特点。比如设计公路，不仅要求方向连续($G^1$)，而且还要求曲率连续。因此，求导是bezier曲线的一项基本而且重要的功能。

1.导数公式的推导

bezier曲线的矩阵形式如下：

$$C(u) = \begin{bmatrix}B_0&B_1& \cdots & B_n\end{bmatrix}\begin{bmatrix}P_0\\P_1\\ \cdots \\ P_n\end{bmatrix}$$ 因为参数只存在于矩阵左边部分，因此分别对基函数求导即可。按照基函数的定义形式，对参数u求导，并且将结果重组，可以得到如下形式： $$B_{n,i}^\prime(u) = n(B_{n-1,i-1}(u) – B_{n-1,i}(u))$$ 当i=0时，$B_{n-1,i-1}(u)=0$  为了表达简便，令$b_i = B_{n-1,i}(u)$ $$C^\prime(u) = n \begin{bmatrix} b_0& \cdots & b_{n-1} \end{bmatrix} \begin{bmatrix} P_1 \\ \cdots \\ P_{n}  \end{bmatrix} +  n\begin{bmatrix} b_0& \cdots  & b_{n-1} \end{bmatrix} \begin{bmatrix} -P_0 \\ \cdots  \\ -P_{n-1} \end{bmatrix} =\\ n\begin{bmatrix} b_0& \cdots & b_{n-2} & b_{n-1} \end{bmatrix} \begin{bmatrix} P_1-P_0 \\ \cdots \\ P_n-P_{n-1}  \end{bmatrix} =  n \sum_{i=0}^nB_{n-1,i}(u)(P_{i+1}-P_i)$$ 共n-1项。可见，n阶bezier曲线的导数是由n-1阶bezier曲线得到的。对应n阶曲线上u的切矢量为n-1阶曲线上的u点的值。而这个导数构成的曲线的控制点序列为 $$Q_i = n(P_{i+1}-P_i) ; i \in [0,n-1]$$

2.导数的计算

已知n阶bezier曲线的导数是n-1阶bezier曲线 $C^{\prime}(u) =sum_{i=0}^nB_{n-1,i}(u)Q_i$，因此bezier曲线的求导可以转换为对低阶曲线的求值操作，可用德卡斯特里奥(De Casteljau’s)算法计算。

3.bezier首尾点的导数

在bezier曲线的定义中我们推导过，bezier曲线的首尾点与其首个，末尾控制点重合。因为bezier曲线的导数也形成bezier曲线，因此在u=0时的导数为$n(P_1-P_0)$，在u=1时的导数为$n(P_{n}-P_{n-1})$，也就是说，曲线在首尾处的切线与其首个、末尾处的控制点的方向是一致的！这是一个非常棒的性质，使得bezier曲线的修型更简单了，无怪乎得到了设计人员的青睐。下图可以看到这种现象：

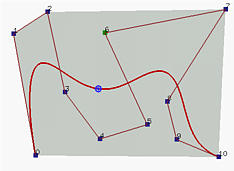
4.连接两根bezier曲线并保证方向一致

当图像由多个bezier曲线构成，并且要求曲线接头的时候方向连续（$C^1$）。比如，要求m阶bezier曲线($P_0,\cdots,P_m$)与n阶bezier曲线($Q_0,…,Q_n$)在$P_m$与$Q_0$连续，首先要求$Q_0=P_m$,然后 导数相等 $m(P_m-P_{m-1}) = n(Q_1-Q_0)$。这说明三点共线，并且满足一定的模长关系达到$C^1$。如下图：

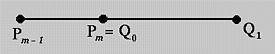
当三者仅共线时，曲线满足$G^1$。$C^1$与$G^1$的区别可以打个比方，假如曲线为两段公路，$C^1$曲线可以保证方向和速度连续变化，但是$G^1$曲线只能保证方向连续。

当m=n时，当且仅当$P_{m-1}P_m$与$P_mQ_1$的长度一样并且三者共线时，曲线保证$C^1$连续。我用coreldraw学习做地图时，感觉coreldraw的bezier曲线的工具非常好用。它用一个等长度的手柄保证bezier接头处方向连续。如下图中的虚线：

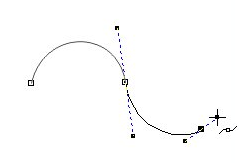
手柄的端点即为控制点。默认接边时，调节鼠标所在端点时，其对称的控制点也会相应移动保证方向连续。其中的数学原理估计很多设计人员是不了解的，但是丝毫不影响coreldraw成为非常易用的工具，这就是好的产品的特点。

5.高阶导数

参数曲线的m阶导数的递推公式为m-1阶导数曲线的一阶导数。

$$f^{(m)}(u)=\frac{d}{du}f^{(m-1)(u)}$$ 以bezier的二阶导数为例， $$C^{\prime\prime} = \sum_{i=0}^{n-2}B_{n-2,i}(u)\{(n-1)(Q_{i+1}-Q_i)\} \\ =(n)(n-1)\sum_{i=0}^{n-2}B_{n-2,i}(u)\{P_{i+2}-2P_{i+1}-P_i\}$$

以此类推。

6.bezier曲线的打断

所谓打断bezier曲线，是指在给定参数u处，将原bezier曲线分成两段，其形状保持不变，阶次保持不变，打断后的两段仍然是bezier曲线。但是，每一段曲线有自己新的控制点序列与参数区间，原来的$u\in[0,1]$分裂为独立的$t\in[0,1];r\in[0,1]$。

德卡斯特里奥(De Casteljau’s)算法  可以用来完成新控制点的计算，回想一下，deCasteljau方法进行对原始控制点进行n次“切角”运算，最后一次切角的结果就是对应u的点。其实，每个迭代形成的新的点列的首点与尾点，分别构成了在u处打断的两条beizier曲线的新控制点序列。如下图示，黑色线是左侧bezier曲线的新控制点，红色线是右侧bezier的新控制点。

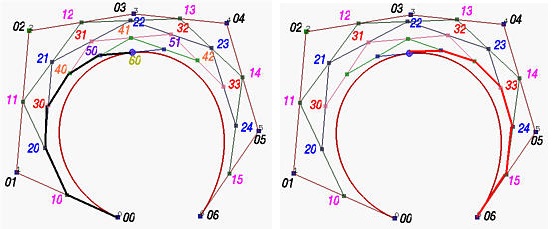
我的算法实现如下：

/*!
 *\brief Bezier曲线的打断
*\ param const std::vector<Point> & control_vertex 控制点序列
*\ param double u 打断处的参数 (0,1)
*\ param std::vector<Point> & cv_left 打断后前半部分的控制点
*\ param std::vector<Point> & cv_right 打断后后半部分的控制点
*\ Returns:   void
*/
void Bezier::Subdividing(const std::vector<Point>& control_vertex, double u,std::vector<Point>& cv_left,std::vector<Point>& cv_right)
{
	cv_left.resize(control_vertex.size());
	cv_right.resize(control_vertex.size());

	int p = control_vertex.size()-1;
	//将 cv 拷贝到 cv_right,因为每次迭代计算的点数依次少1，
	//因此可以直接用cv_right记录，全部算完后就是所有的尾点集合
	std::copy(control_vertex.begin(), control_vertex.end(), cv_right.begin());
	cv_left[0] = cv_right[0];

	//p次迭代
	for (int i = 0;i<p;++i)
	{
		for (int j = 0;j<p - i;++j)
			cv_right[j] = (1.0 - u)*cv_right[j] + u*cv_right[j + 1];
		//左侧控制点为每次迭代的首点
		cv_left[i + 1] = cv_right[0];
	}
}

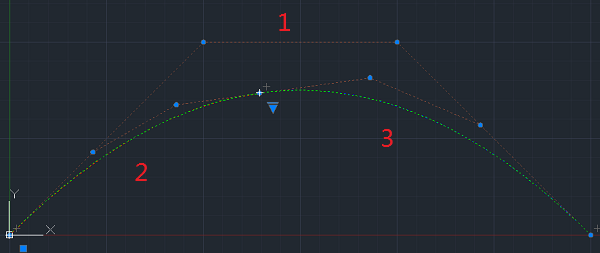
下图是上述程序对bezier曲线在$u=0.4$打断后的效果 写入dwg在AutoCAD中的展现。1为原始bezier曲线，2,3为打断后bezier曲线。

---

本节参考 Introduction to Computing with Geometry 第五，六节