计算机图形学中，我们已经接触了贝塞尔曲线的定义。在这篇文章里，我将从几何意义出发解释bezier曲线的定义与运用，为nurbs的学习奠定基础。

bezier曲线的目的

设计人员寻找的是更加“几何”的参数曲线，即系数具有直接的几何含义，能够通过参数直接预测几何形状以及变化趋势的曲线。这样的曲线需要具备以下特征：

1. 直观，曲线的算法应具备几何意义。
2. 灵活，曲线的创建，修型应提供更灵活的方式，并且创建，修改的方式应该更像是几何操作，而不是修改方程。
3. 统一方法，曲线能够表现各种基本形状及其组合，并且，修改这些形状的方式应该是统一的。
4. 高效且具备数值稳定性。

贝塞尔曲线，样条曲线、nurbs 这一类曲线较好的解决了上述问题，成为各类辅助设计软件(coreldraw，AutoCAD等)广泛应用的一类曲线，他们的共同特征是：

1. 引入了“控制点”的概念，通过控制点的形状分布，能够确定曲线的走势，修改控制点（以及其他参数），可以影响曲线的形状，操作直观，不需要直接修改方程。
2. 用户可以任意的添加控制点，而不改变曲线的形状，这样，曲线的自由度增加，曲线修型十分方便。
3. 曲线具有打断，连接的能力。
4. 曲线到曲面的扩展非常的容易。

bezier曲线的定义：

给出\(n+1\)个控制点\(\{P_0,P_1,…,P_n\}\)，n阶贝塞尔曲线的定义是 \(C(u)=\sum_{i=0}^{n}B_{n,i}(u)P_i\)。系数\(B_{n,i}(u)\)的定义是：$$B_{n,i}(u) = \frac{n!}{i!(n-i)!}u^i(1-u)^{n-i}$$还记得高中数学知识的同学要笑了，嘿嘿，这个不是二项式\((u + (1-u))^n\)的展开式么，真被你猜对了。得到这个观察，bezier曲线的一些重要的性质就特别好理解了。

用矩阵形式表达的bezier曲线是这样的 $$C(u) = \begin{bmatrix}B_0&B_1& \cdots &B_n\end{bmatrix}\begin{bmatrix}P_0\\P_1\\ \cdots \\ P_n\end{bmatrix}$$之所以这么写是为了表达bezier是所有控制点线性组合的结果。左侧的函数称为基函数，右侧的点称为贝塞尔曲线的“控制点”。参数u的定义域为[0,1],因此，所有的基函数都是非负的。因为u与i都可能为零，我们规定\(0_0=1\)。

贝塞尔曲线有如下重要的性质。

1. n+1个控制点的度数为n。
2. 曲线通过\(P_0\)与\(P_n\)。当u=0时，曲线通过\(P_0\),当u=1时，曲线通过\(P_n\)，这比较方便做形状的控制。
3. 非负性，所有的基函数都是非负的。
4. 归一性，在某个特定的参数u处，所有的基函数的和加起来都等与1。前面我们说过 基函数其实是二项式\((1+(1-u))^n=1^n\)的展开式，其加和肯定等与1。下图是四阶bezier曲线的基函数图像。
5. 
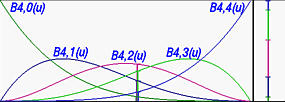
6.  凸包性质，曲线处在所有控制点所决定的凸包之内，并且只有首尾点位于凸包之上。这个性质在bezier转折线，bezier空间范围判断等计算上非常有用。
7. Variation Diminishing Property：这一条真心不知道怎么翻译，意思就是一条直线与bezier的交点数量一定不大于直线与曲线控制多边形交点的数量。如果曲线为空间曲线，将线替换成平面同样可以满足上述性质。这条性质说明的是bezier曲线的扭转和弯折的情况要比其控制多边形要轻微。
8. 仿射不变性：如果需要对bezier曲线做仿射变换，只需要对其控制点序列进行仿射变换即可。其基函数（矩阵形式的左半部分）不需要变化。这个性质使得bezier曲线对于图形变化非常友好。

参数定义域不在[0,1]的贝塞尔曲线

对于定义域不在[0,1]内的贝塞尔曲线，可以通过拉伸的方式将其映射到[0,1]，假设定义域为[a,b]的曲线，其基函数的形式为$$B_{n,i}(u) = \frac{n!}{i!(n-i)!(b-a)^n}(u-a)^i(b-u)^{n-i}$$

移动控制点

如果移动某控制点\(P_k\)到新位置\(P_k+\vec v\),那么bezier曲线的形状将发生什么样的变化呢？假设新的bezier曲线是\(D(u)\)，$$D(u) = \begin{bmatrix}B_0& \cdots &B_k& \cdots &B_n\end{bmatrix}\begin{bmatrix}P_0\\\cdots \\P_k+\vec v\\ \cdots \\ P_n\end{bmatrix} = C(u) + B_k\vec v$$即新曲线的每个点的移动距离为其对应的参数u的基函数\(B_k(u)\)乘以移动向量\(\vec v\)。曲线移动的方向都是一致的(基函数非负)，在\(B_k(u)\)达到最大值时，移动的距离达到最大值。而且因为基函数小于等于1，曲线上每个点的模长均小于等于\(|\vec v|\)。

本文参考Introduction to Computing with Geometry 的第五章 Bezier Curves 的前三节。