给定2D平面上点\(c(x,y)\)确定其是否在多边形p内部，是比较常见的几何查询问题之一。本文的内容是阐述射线法(Ray Casting Algorithm)求解普通多边形(simple polygon) PIP(point in polygon)问题的思路与实现。目前网上类似文章不少，但是其中部分文章缺乏对特殊情况的讨论，在应用时容易在特例数据上失败。

算法思路：

ray casting 算法也称之为 crossing number 算法或者 even-odd rule 算法，主要实现思路基于这样的观察，如果从 点  c 出发做一条任意方向的射线，射线将与多边形 p 相交于若干交点 \(p_0,p_1,…,p_n\)。交点的个数为奇数时点在多边形内（点在多边形上也算多边形内）；反之点在多边形外。前提是多边形必须为普通多边形(simple polygon)。

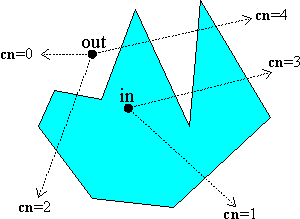
为了计算简便，通常采用的射线为自点c水平向右的射线。

特殊情况的讨论：

当射线经过多边形的边时，会出现如下情况（如图所示）：

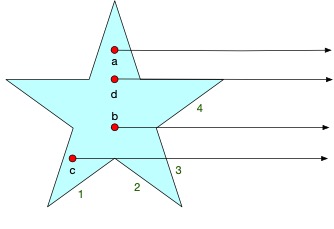
1.点a 所在射线经过多边形的非端点，交点有效，计数为1。

2.点b所在射线经过多边形上边的端点，交点有效，计数应该为1。

3.点c所在射线经过多边形上边的端点，但此端点应计为无效交点，计数为0。

4.点d所在射线经过多边形上的水平边(horizontal line),无效端点，计数为0。

如何区分2.3.两种情况？ 不妨定义射线与端点相交的规则如下：

当相交端点是 所在边的 下端点（y值较小）时记录为有效交点，计数为1，当相交端点是所在边的上端点（y值较大）时记录为无效端点，计数为0。反之亦可。

因此点b对应的情况为与边4存在交点，与边3不存在交点，总交点数为 1。

点c对应的情况为点c与边1边2 的交点均为上端点，总交点数为0。

c++实现：

我的代码地址：https://github.com/whudongjian/spatial_overlay/blob/master/algorithm/gemetry_util.cpp

bool GeometryUtil::point_in_polygon(const overlay::geometry::Coordinate &c, overlay::geometry::LineString *ring)

参考文献：

1.inclusion of a point in polygon .geomalgorithms.com

2.simple polygon . wikipedia.