本文介绍两种多边形（简单多边形）的顺逆时针顺序判断算法，其中一种算法就是通过计算多边行的面积(带符号)来判断。另一种方法是根据最左侧点前后边的转向(叉积)判断。有意思的是，网上有一些文章并没有就这种方法的特殊情况进行讨论。

1.多边形的面积算法

多边形的面积算法可以由三角形的面积算法引出。先看三角形的面积计算

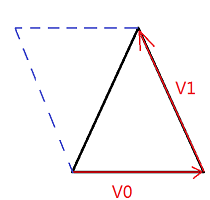
$$Area(\Delta) = \frac {\vec v_0 \times \vec v_1}{2}$$

实际上，向量的叉积为向量，在二维几何情况下，我们将其当做标量时，指的是向量的Z维。叉积是由符号的，当三角形位于向量的左侧时，任意两边求解的面积均为正号。

多边形的面积即将多变形分解为若干三角形的面积加和: $$\begin{equation*}
s = \sum_{i=1}^{n-3}{Area(\Delta c_0c_ic_{i+1})}
\end{equation*}$$

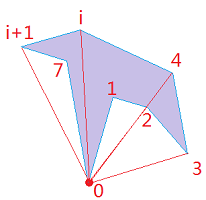
其中，n值多边形boundary节点个数，按照惯例尾点与首点重复，即三角形有4个节点。当多边形环序为逆时针顺序时，面积为正，反之为负号。因此，当多边形存在“洞”时，面积公式只需要将洞的环构成的面积加入即可。洞的顺序与外环顺序是想反的，因此形成的面积会相减。

1.1对比：

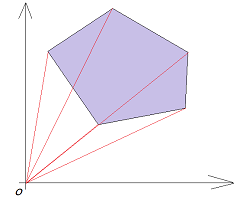
一种相似的方案如上图所示。$$\begin{equation*}
s = \sum_{i=0}^{n-2}{Area(\Delta c_0c_ic_{i+1})}
\end{equation*}$$ 你能知道这个方法最大的问题么？其实，这个方法的问题在于，如果多边形位于原点位置较远，而坐标存储精度不够大的情况下(如使用float保存)，容易出现比较大的摄入误差，因为由原点与边构成的多边形面积过大，计算叉积的时候还有可能因为溢出而计算不正确。所以不推荐使用。其实第一种方法就是为了避免这样的情况发生，从而将原点移动到了多边形第一个节点处。

1.2 实现代码

double Algorithm::LineRingArea(const std::vector<Coordinate>& input)
{
	if (input.size() < 4)
		return 0.0;
	double area = 0.0;
	const Coordinate& c0 = input.front();
	for (int i = 1, n = input.size(); i < n - 2;++i)
	{
		Vector v0 = input[i] - c0;
		Vector v1 = input[i + 1] - input[i];
		area += v0.CrossProduct(v1).z;
	}
	return area/2.0;
}

 

2 多边形的顺逆时针顺序判断

2.1 面积法

根据第一节描述，如果多边形为逆时针顺序，面积为正；反正面积为负；

2.2 根据最左侧点上下边的走向判断

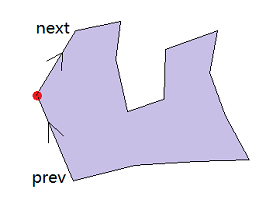
据上图，如果从最左侧点(leftmost)看，其前一条边与后一条边的转向关系为右转，那么多边形为顺时针顺序。反之，如果转向关系为左转，则多边形为逆时针顺序。转向关系可以用两条边的向量的叉积判断。

wait a minute……  我们还漏掉了某种特殊情况，如果说面的最左侧点的x坐标与prev，next 点的坐标相同，即两条边共线呢？ 这种情况是一种特殊情况(“degenerate case”)。

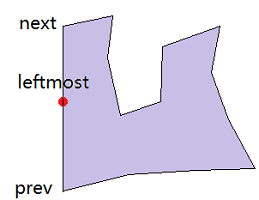
因为三个点的x值是相同的，因此完全有可能出现 中间的点被选为leftmost point从而引发判断问题的。

解决方案就是判断 prev ,next 点的上下关系(y值)。若 \(y_{prev} < y_{next}\)则多边形为顺时针顺序。反正为逆时针顺序。

综上，依据最左侧上下边走向判断多边形顺序的算法是：

找到最左侧点\(P_i\)。

计算 向量叉积 \(\vec{P_{i-1}P_{i}} \times \vec {P_iP_{i+1}}\)。若 叉积<0,多边形为顺时针顺序；若叉积>0 ，多边形为逆时针顺序；

若叉积等于0: 若 \(P_{i-1}.y < P_{i+1}.y \) 则 多边形为顺时针顺序，否则多边形为逆时针顺序。

实现代码：

bool compare_x(const Coordinate& p0, const Coordinate& p1)
{
	return p0.x < p1.x;
}
bool Algorithm::IsCCW(const std::vector<Coordinate>& input)
{
	int n = input.size();
	int leftmost = std::distance(input.begin(), std::min_element(input.begin(), input.end(), compare_x));
	int prev = leftmost - 1;
	if (prev < 0) prev = n-2; //倒数第二个点
	int next = leftmost + 1;
	if (next >= n) next =1; //正数第二个点

	Vector v0 = input[leftmost] - input[prev];
	Vector v1 = input[next] - input[leftmost];
	double orientation = v0.CrossProduct(v1).z;
	if (orientation == 0)
	{
		return input[prev].y > input[next].y;
	}
	else
	{
		return orientation > 0;
	}
	return true;
}

3.参考文献：

1.Berg M D, Cheong O, Kreveld M V, et al. Computational Geometry: Algorithms and Applications[M]. Springer Publishing Company, Incorporated, 2000. 第三版 第36页

2.geos 中geos::algorithm::CGAlgorithms::IsCCW(.)函数的实现；